有意差検定の解説

1 有意差検定とは
2 検定の手順
3 検定の種類
4 比率の検定
- 4.1 Ａ．サンプルが異なる場合
- 4.2 Ｂ．同じサンプルの場合

有意差検定とは

有意差検定とは、アンケート集計の結果からある２つの値の間に統計的に意味のある差があるかどうかを判断するものです。たとえば、ある会社の担当者が行った調査で、東京と大阪でのある新製品Ａの使用率はそれぞれ３０％と２０％という結果が出たとします。この１０％の差から、社長へのプレゼンで「東京と大阪での新製品Ａの使用率には差がありました。」と言い切るためには統計的裏付けをとらねばなりません。その裏付けとなる判断をするのが有意差検定（有意性検定）です。

検定の手順

検定の手順としては、まず東京と大阪での使用率は同じであるという仮説をたてます（帰無仮説と言います）。ここで、実際の調査結果から２地域での「使用率が同じになる」確率を計算します。この確率が十分に小さければ使用率は同じであるという仮説を捨てて、「使用率は同じではない（＝差がある）」、すなわち統計的にみて有意差があるとみなすことができるのです。なお、捨て去った「使用率は同じになる」確率のことを有意水準または危険率という。たとえば５％の有意水準とは、５％の確率で使用率に差があるという判断は誤りますよ、ということを意味します。また、この「５％の有意水準」を、「９５％の信頼度」と言い換えることができます。９５％の信頼度で有意差があるということは、上記の例では、「９５％の信頼度（確かさ）で東京と大阪での新製品Ａの使用率には差があります。」と社長にプレゼンすることができるのであります。

検定の種類

有意差検定は、調査結果のデータの種類が平均値か比率（パーセント）か、比較するデータが異なる対象者のものか同じ対象者のものか等によって主に、（１）比率の検定（２）平均値の検定（３）度数の検定の３つの方法に分けられます。この中でもマーケットリサーチで頻繁に使われるのが（１）比率の検定と（２）平均値の検定です。比率の検定は、サンプル数と比率の２種類のデータから行うことができますが平均値の検定にはサンプル数、平均値、平均値の標準偏差　（異なる対象者から得られたデータの場合）、さらに同じ対象者から得られたデータの場合（1対比較、ｐａｉｒｅｄ　ｔｅｓｔなど）には、同一対象者の２つの平均値の差の標準偏差値などが必要となります。

比率の検定

比率の検定は、文字通り２つの比率（パーセント）の差を検定するものです。そして、この２つの調査データ(比率）が異なるサンプル（対象者）のものか同じサンプルのものかによって異なる計算方法が用いられます。

Ａ．サンプルが異なる場合

検定式は次のようになります。

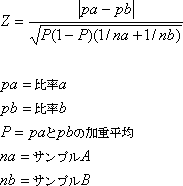
例えば、東京に住んでいる人（３００人）と大阪に住んでいる人（２００人）のある新製品Ａの使用率が、それぞれ３０％と２０％であったとします。この１０％の差が統計的に意味のある「差」であるかどうか検定する式は次のようになります。

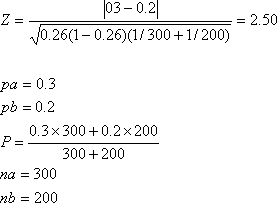
このＺの値を（近似的に正規分布するものとみなし）正規分布表と比べ有意差があるか否か、どのくらいの有意水準で有意差があるかを判断します。（正規分布についての説明は割愛させていただきます）
正規分布表では、
Ｚ＝２．５７６のとき有意水準１％で有意差あり
Ｚ＝１．９６０のとき有意水準５％で有意差あり
Ｚ＝１．６４５のとき有意水準１０％で有意差あり
となっています。（自由度=∞のとき）
上記の例ではＺ＝２．５０なので、５％の有意水準で有意差ありと判断できます。言い換えれば９５％の信頼度（確かさ）でこの１０％の差は統計的に意味のある差であると言えるのです。
↓ウェブ上で異なるサンプル間の有意差検定が実行できるツールです。
異なるサンプル間の有意差検定

Ｂ．同じサンプルの場合

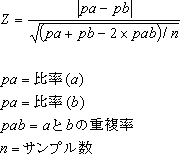
例えば、東京に住んでいる人（３００人）の新製品Ａと新製品Ｂの使用率が、それぞれ３０％と２０％であったとします。そして、ＡとＢの両方を使用している人の割合は１０％であったとします。この１０％の差が統計的に意味のあるかどうか検定する式は次のようになります。

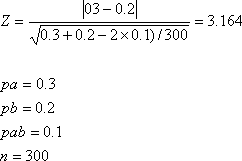
このＺの値を（近似的に正規分布するものとみなし）正規分布表と比べ有意差があるか否か、どのくらいの有意水準で有意差があるか判断します。
正規分布表では、
Ｚ＝２．５７６のとき有意水準１％で有意差あり
Ｚ＝１．９６０のとき有意水準５％で有意差あり
Ｚ＝１．６４５のとき有意水準１０％で有意差あり
となっています。（自由度=∞のとき）
上記の例ではＺ＝３．１６４なので、１％の有意水準で有意差ありと判断できます。言い換えれば９９％の確かさでこの１０％の差は統計的に意味のある差であると言えるのです。

＊なお、この比率の検定は、サンプル数がある程度大きくないと比率の分布が正規分布しないため、通常サンプル数３０以上を前提として検定されます。（当サイトのプログラムでは、サンプル数３０以下はエラーになります）

クロス集計表の見方
弊社で作成する集計表でどのように有意差検定が表示されるかご覧になれます。